Графічна робота 2. Тема: Лекальні прямі. Спряження.
Завдання 1.Перегляд за посиланням.
https://www.youtube.com/watch?v=qgKFz99iz9s
Завдання 2. Побудова профілю кулачка
Умова. Побудувати профіль кулачка та дотичні до двох лекальних кривих, які не використані в завданні.
Графічну роботу виконують на аркуші формату АЗ (297x420). Приклад виконання на рис. 23.
Побудову профілю кулачка в кожному варіанті потрібно починати з нанесення осей координат Ох та Оу. Потім будують лекальні криві по їх заданим параметрам та виділяють їх ділянки, які входять в профіль кулачка. Після цього можна будувати плавні переходи –
спряження | між | лекальними | кривими. |
| |
Позначення Rх зазначає, що величина радіуса |
| ||||
визначається побудовою. На кресленні слід |
| ||||
проставити певний розмір зі значком “*”, |
| ||||
наприклад R20*. |
|
|
| ||
Спряження – це плавний перехід від однієї |
| ||||
лінії (прямої або кривої) до другої (кривої або | РРис. 2.9 | ||||
прямої). Перехід буде плавним тільки в тому | |||||
Рис. 1.27. | |||||
випадку, коли в спільній точці, яка називається | |||||
Приклад | |||||
| Рис. 9 |
|
| виконання | |
точкою дотику, дотичні обох ліній збігаються в | завдання 7 | ||||
одну пряму. Побудувати спряження – це означає знайти центри дуг спряження та точки спряження.
Побудова спряження базується на відомих положеннях геометрії: пряма, яка сполучає центри дотичних дуг, проходить через точку дотику (точка А рис. 9), а дотичні цих дуг в точці А співпадають (t1 ≡ t); пряма, дотична до кола, утворює прямий кут з радіусом, проведеним в точку дотику. В контурах технічних деталей використовуються плавні переходи від прямої до дуги кола та від дуги одного радіуса до дуги іншого радіуса. В останньому випадку виникає поняття внутрішнього та зовнішнього спряження. Спряження є
внутрішнім або зовнішнім, якщо центри заданих кіл розміщенні, відповідно, всередині або зовні повного кола спряження, побудованого з центру спряження радіусом спряження.
Спряження двох прямих дугою заданого радіуса. Центр Оs дуги спряження радіуса Rs (рис. 10) має бути віддаленим на відстань Rs як від прямої а, так і від прямої b, тобто розміщуватись у точці перетину прямих с і d, відповідно паралельним прямим а і b. Для визначення точок спряження (дотику) А і В слід з точки Оs опустити перпендикуляри на прямі а і b.
а | б | в |
11
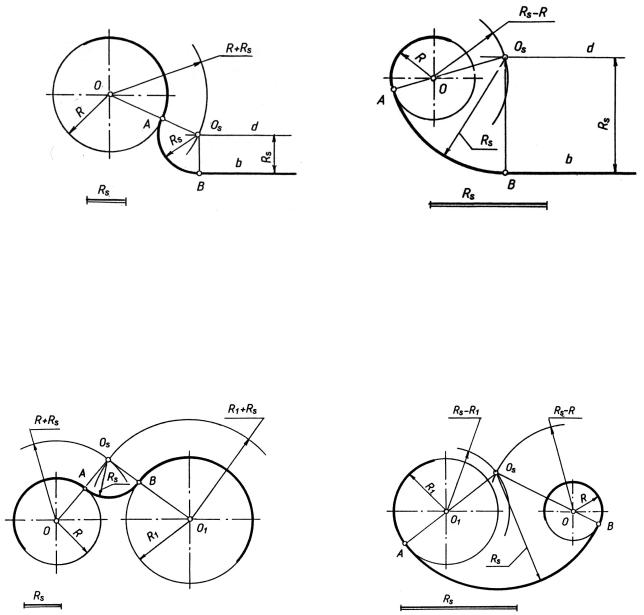
Рис. 10
Спряження кола з прямою дугою заданого радіуса. Можливе зовнішнє (рис. 11) та внутрішнє (рис. 12) спряження.
Центр Оs дуги спряження радіуса Rs має бути віддаленим на відстань Rs від прямої b та кола радіуса R, тобто знаходитись в точці перетину прямої d, яка паралельна до заданої прямої і віддалена від неї на відстань Rs та кола певного радіуса, який дорівнює R + Rs у випадку зовнішнього спряження (рис. 11) або Rs - R у випадку внутрішнього спряження (рис. 12). Для визначення точок спряження А та В слід з точки Оs слід опустити перпендикуляр на пряму b та сполучити центр спряження Оs та центр кола О.
Спряження двох кіл дугою заданого радіусу.
Розглянемо три випадки спряження двох кіл.
Зовнішнє спряження. Центр Оs дуги спряження радіуса Rs (рис. 13) має бути віддаленим на відстань Rs від кіл радіусів R та R1 і розміщуватись у перетині двох дуг радіусів R + Rs та R1 + Rs. Точки спряження А та В знаходяться на лініях центрів ОsО та О1Оs.
Внутрішнє спряження. Центр Оs дуги спряження радіусу Rs (рис. 14) знаходиться в перетині двох дуг радіусів Rs - R та Rs + R1. Точки спряження А та В знаходяться на продовженнях ліній центрів ОsО та О1Оs.
Рис. 13 | Рис. 14 |
Внутрішній та зовнішній дотик (спряження). Центр Оs дуги спряження радіуса Rs (рис. 15) знаходиться у перетині двох дуг з центрами Оs радіусу Rs + R та О1 радіусу Rs – R1.Точки спряження А та В розміщуються на лініях ОsО та
Оs О1.
12
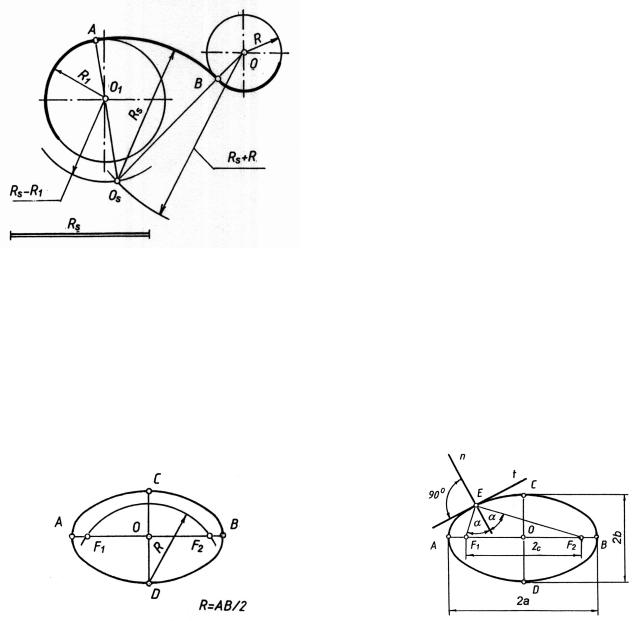
Профіль кулачка складається з відрізків прямих, дуг кіл та лекальних кривих, спряжених між собою. Для побудови спряження прямої або дуги кола з лекальною кривою слід вміти будувати дотичну до лекальної кривої в заданій точці на ній. Розглянемо побудову
дотичної до деяких лекальних кривих.
Еліпс. Для побудови дотичних до еліпса використовують фокуси еліпса. Еліпс є кривою другого порядку і визначається рівнянням другого ступеню: x2/а2 + y2/b2 = 1, де а і b, відповідно, величини великої і малої півосей (рис. 17). Відстань від центру до фокуса можна визначити c2=а2 + b2. На креслениках фокуси еліпса будуються графічно при заданих величинах великої та малої висей (рис. 16).
Рис. 15 | Для |
побудови фокусів еліпса з точки D, граничної точки малої вісі, радіусом, що дорівнює половині великої вісі, будують дугу до перетину з нею. Точки перетину F1 та F2 – фокуси еліпса. Дотична t до еліпса буде перпендикулярна до нормалі n в заданій точці.
Нормаль еліпса (рис. 17) – це бісектриса кута, визначеного довільною точкою на еліпсі і його фокусами. З’єднуємо точку Е з фокусами F1 та F2. Бісектриса кута F1ЕF2, є нормаллю n в точці Е еліпса. Побудувавши через точку Е пряму, перпендикулярну до нормалі n, визначимо дотичну t до еліпса в точці Е.
Рис. 16 | Рис. 17 |
Парабола. Із заданої точки Е будуємо перпендикуляр до директриси параболи і визначаємо точку В. Дотичною t до параболи (рис. 18) в точці Е є бісектриса кута між прямими FЕ та ВЕ, а також перпендикуляр до відрізка BF, побудований з точки Е. Нормаль n у цій точці перпендикулярна до дотичної t.
Гіпербола. Дотичною t до гіперболи в точці Е (рис. 19) є бісектриса кута між прямими F1Е та F2Е , а нормаль n у цій точці перпендикулярна до дотичної t.
13
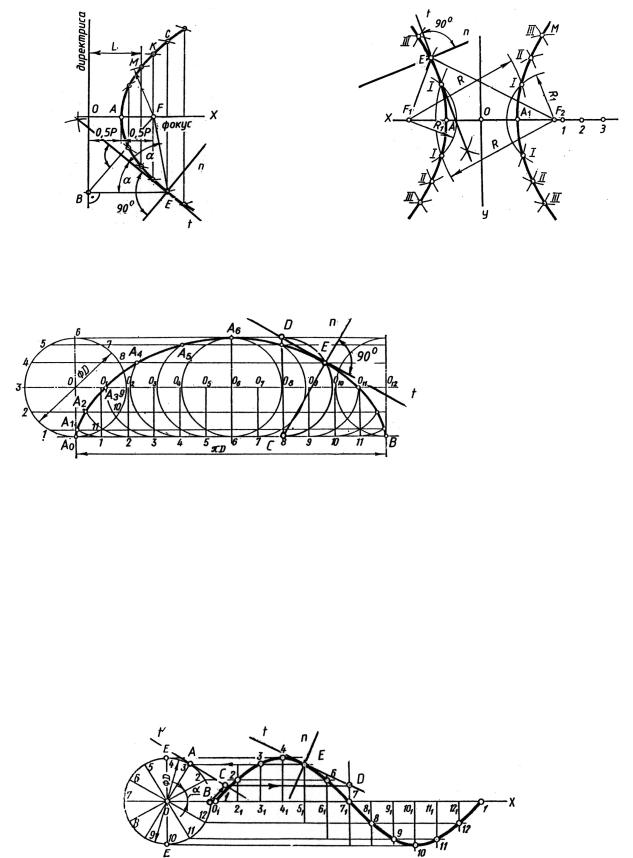
Рис. 18 | Рис. 19 |
|
|
|
Циклоїда. Для побудови дотичної до циклоїди в | заданій точці Е | |||
| визначають | положення | ||
| центру рухомої | центроїди | ||
| (точка 8, рис. 20) заданої | |||
| точки. Через центр О8 | |||
| утворюючого |
| кола | |
| будують | діаметр | СD, | |
| перпендикулярний | до | ||
Рис. 20 | направляючої. Пряма СЕ | |||
визначає нормаль циклоїди | ||||
| в точці Е, а пряма DЕ – | |||
| дотичну. |
|
|
|
Синусоїда. Для побудови дотичної до синусоїди (рис. 21) у заданій точці Е проводять через цю точку пряму, паралельну вісі Ох до перетину з колом (точка А). Через точку А будують дотичну до кола і відкладають на ній відрізок АС , який дорівнює довжині дуги АВ . Через точку С проводять пряму, паралельну вісі Ох до перетину з перпендикуляром до цієї вісі, побудованим з точки перетину синусоїди з віссю Ох , і визначають точку D. Пряма DЕ визначає дотичну t, а нормаль n у цій точці, перпендикулярна до дотичної.
Рис. 21
14
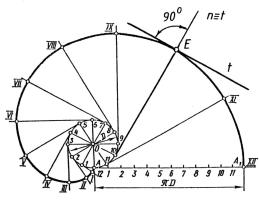
Евольвента. Нормаллю n евольвенти кола в заданій точці Е є дотична tj до кола, побудована з цієї точки. Дотична t до евольвенти в точці Е перпендикулярна нормалі (рис. 22).
|
| Рис. 22 |
|
Розглянуті |
| приклади | побудови |
дотичних | до | лекальних | кривих дають |
можливість |
| будувати | спряження |
прямих, дуг кіл з | лекальними | кривими, а | |
також спряження лекальних кривих між собою.
Немає коментарів:
Дописати коментар